Table of contents
- Before you Begin
- PDFs
- Uses of Mutli-View Geometry
- Background: Structure from Motion (SFM)
- Theory: Solving for camera parameters in the presence of scale ambiguity
- Theory: Epipolar Geometry
- Structure From Motion Step 1: Estimating Fundamental Matrix:
- Triangulation
- Bundle Adjustment
- Final Pipeline Including RANSAC
- Tracking Real World Objects in 3D
Before you Begin
Reference Book 1 Reference Book 2
PDFs
Uses of Mutli-View Geometry
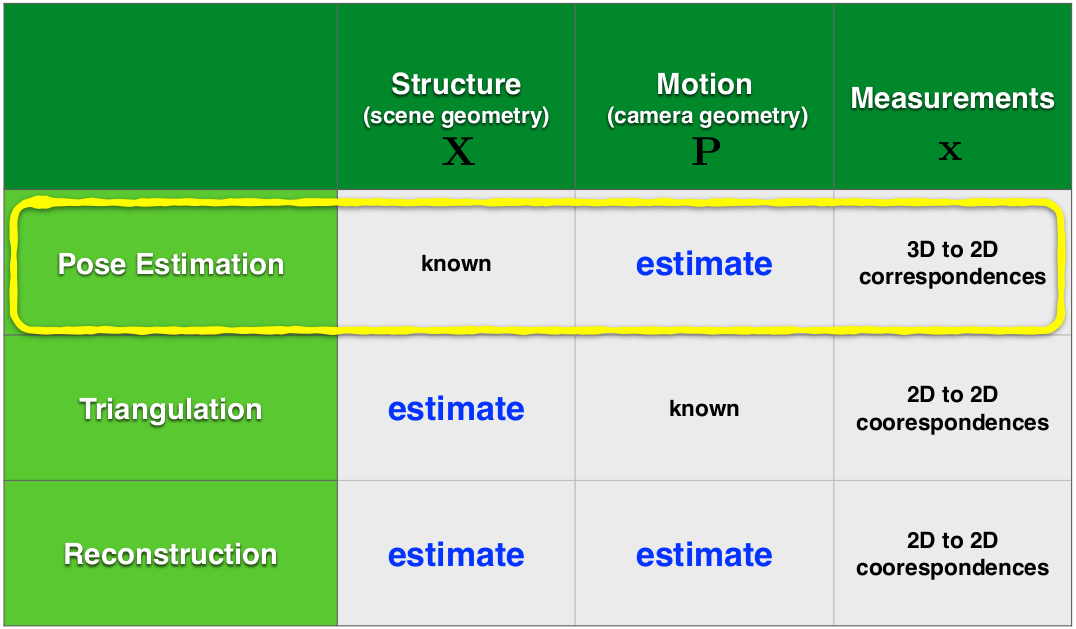
Background: Structure from Motion (SFM)
The basis for classical 3D vision is viewing an object from multiple views to give 3D understanding.
In humans, we don’t have to move to perceive 3D because our eyes(cameras) are already seperated by a fixed distance. This is the same as having one camera move by a fixed distance. Hence, we see “stereo depth vision”
Theory: Solving for camera parameters in the presence of scale ambiguity
Remember we had the following equation:
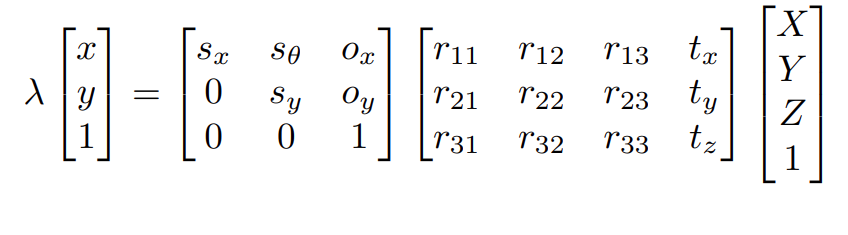
The lambda above is account for a scale factor which is ambiguous. This equation can also be written as:

Solving for Camera Params: Direct Linear Transform
Now, the above equation is a similarity equation. To solve the equation we make use of a neat trick called Direct Linear Transform

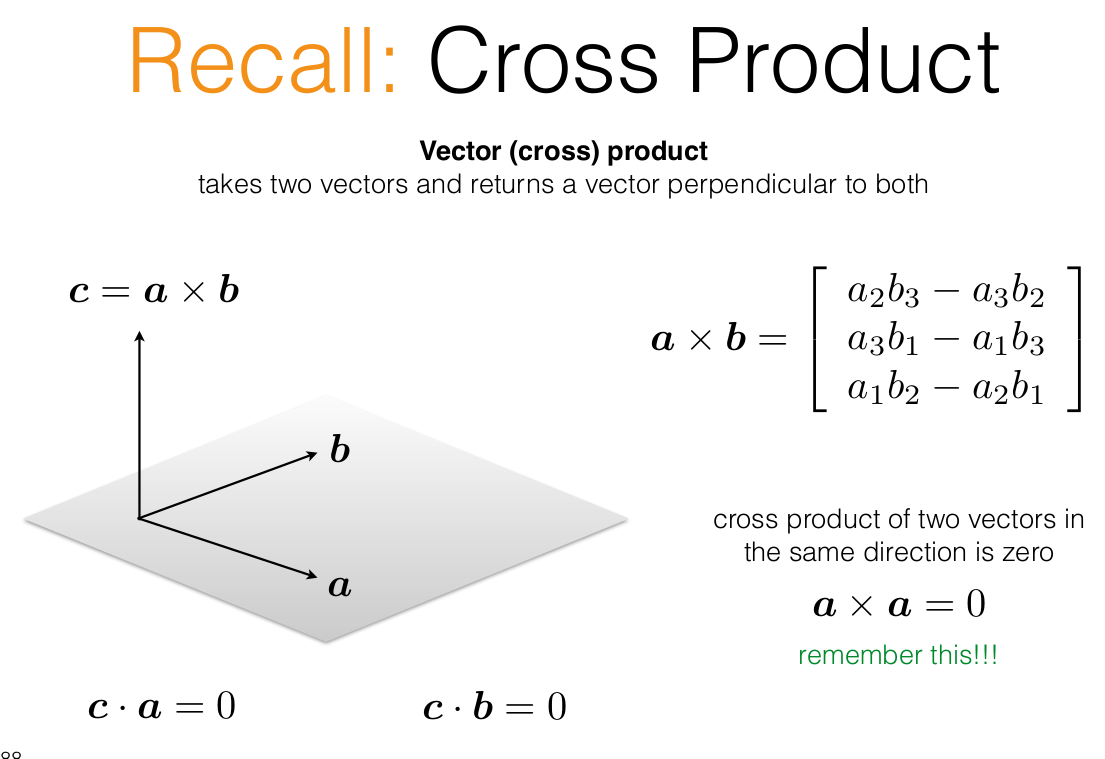
PX should give the same ray (vector) as x, hence their cross product would be zero
Actual Derivation
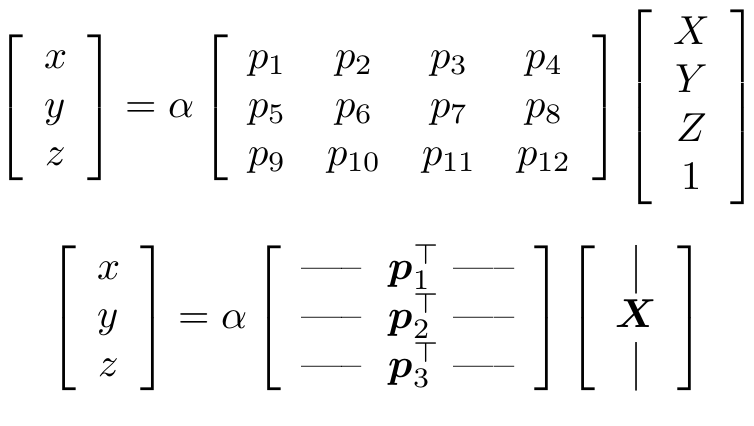
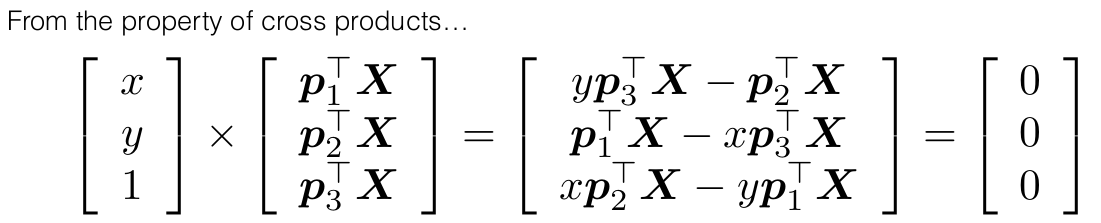

Theory: Epipolar Geometry
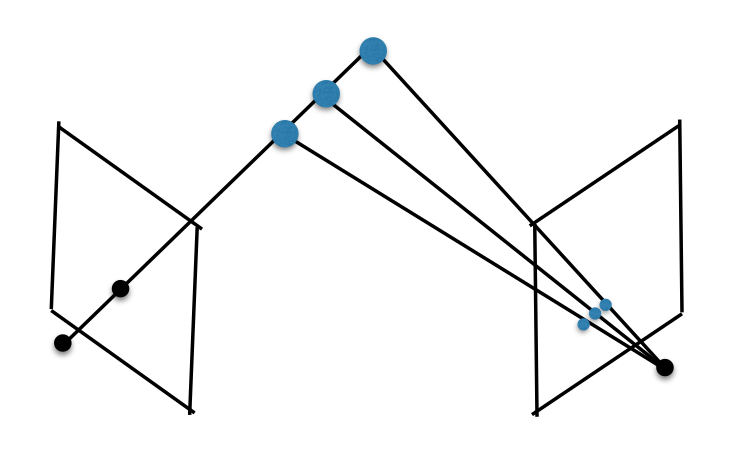
- Simply put, epipolar geometry maps a point in one view, to a line in another view
- Epipolar Geometry is purely determined by camera intrinsics and camera extrinsics
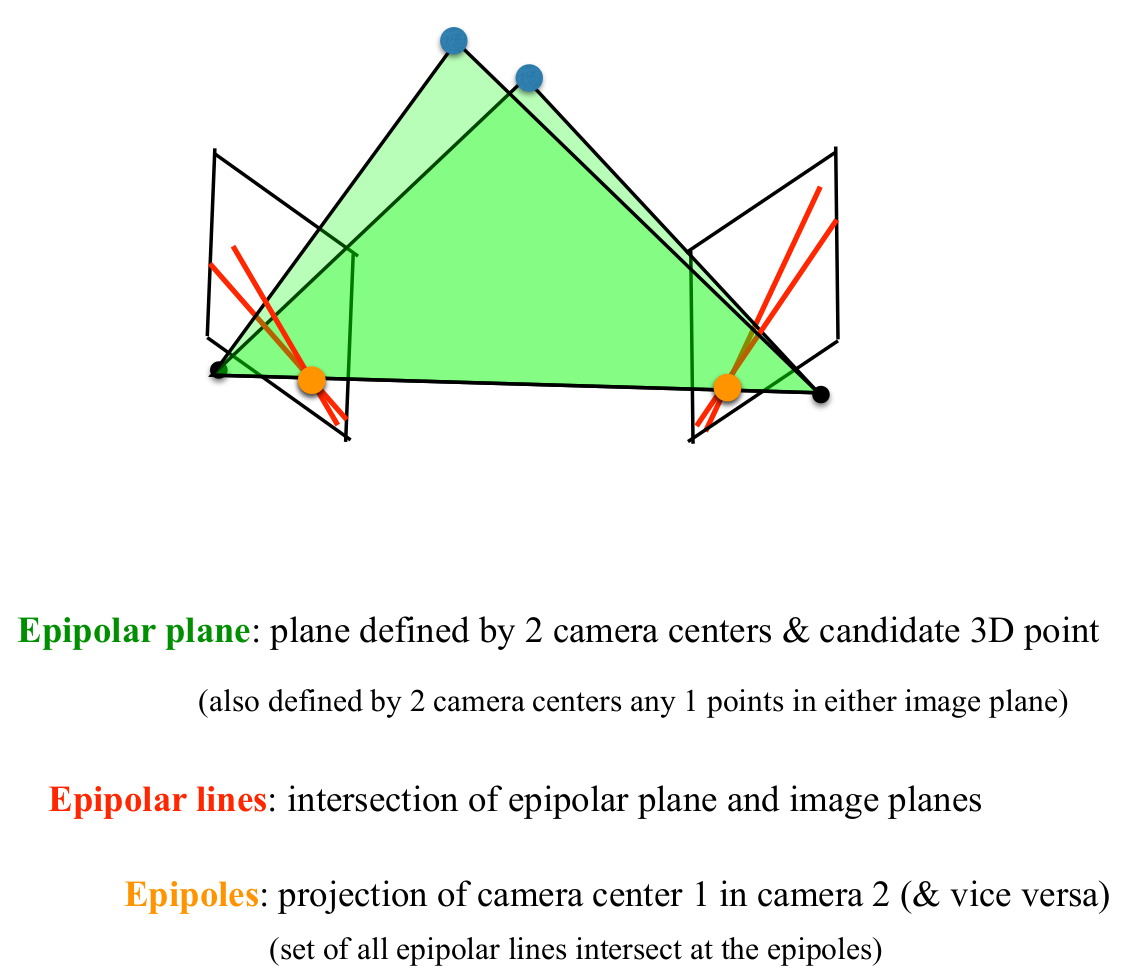
Essential Matrix: Maps a point -> to a line
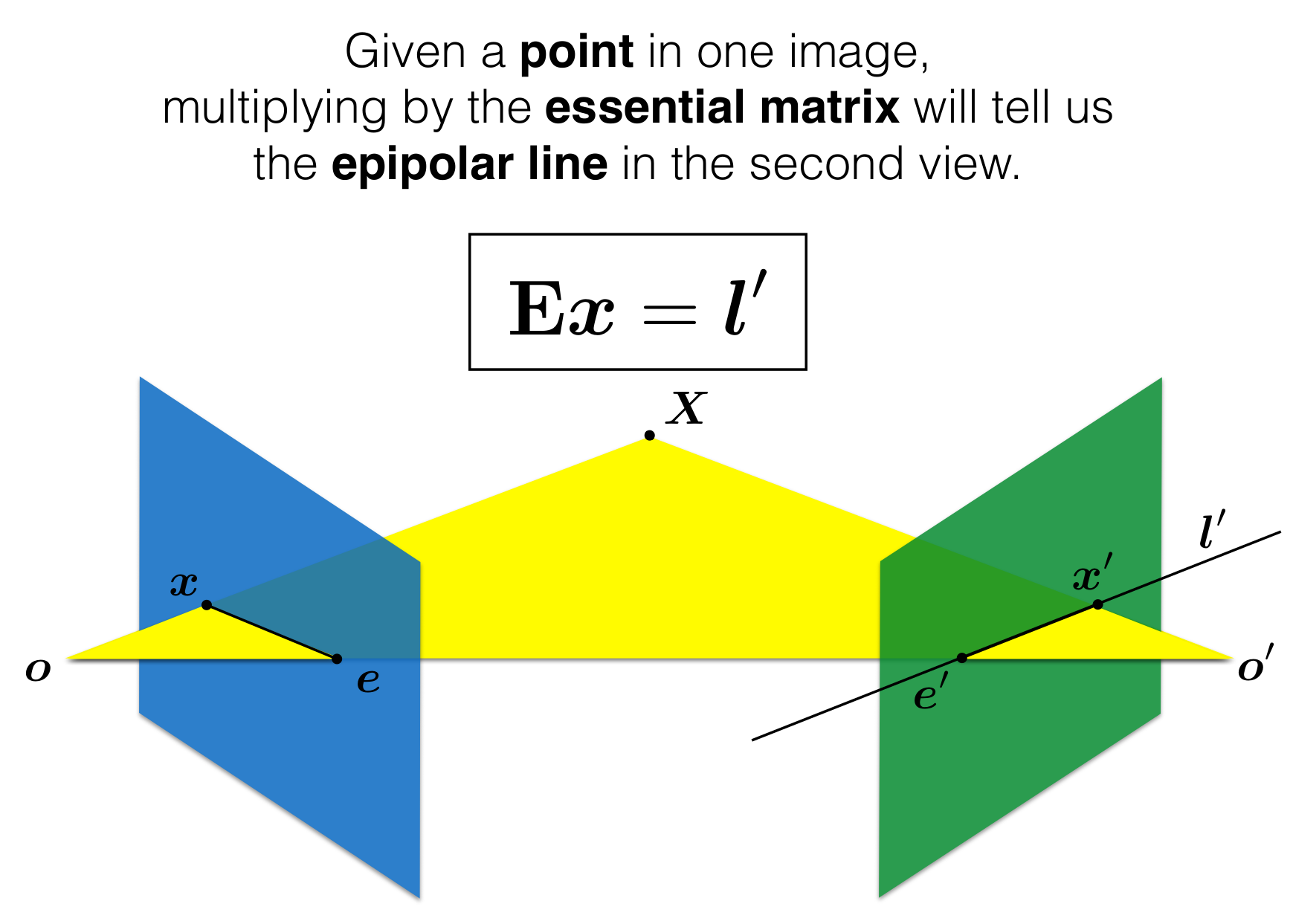
Derivation of Essential Matrix: Longuet Higgins
-
Recall the skew-symmetric form of a matrix can encode cross products
-
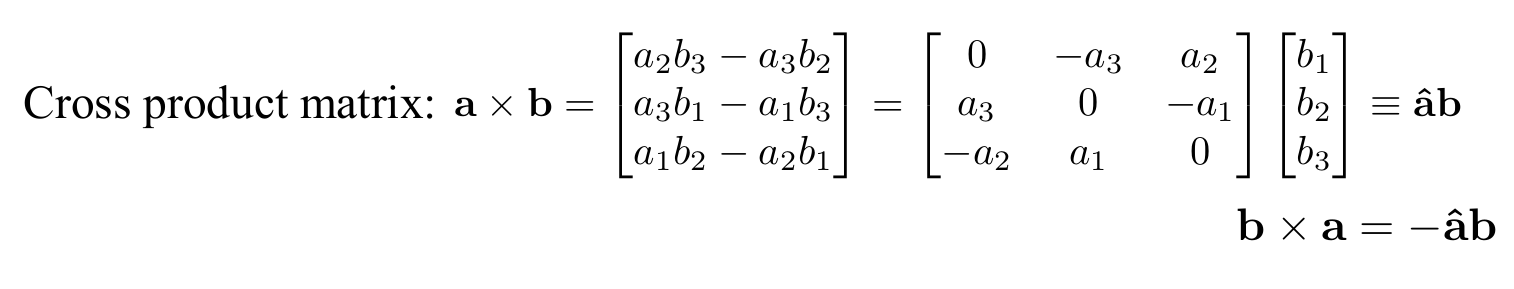
-
We can use this to show how three vectors can define the volume of a parallelpiped:
-
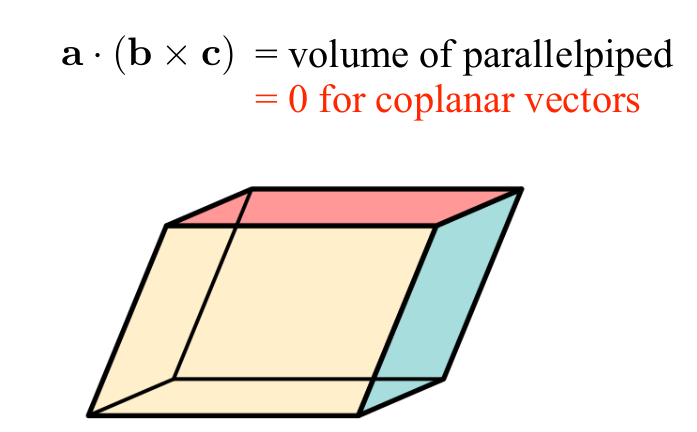
-
Now, given a calibrated camera (i.e. known intrinsics) we can capture a 3D point in two views
-
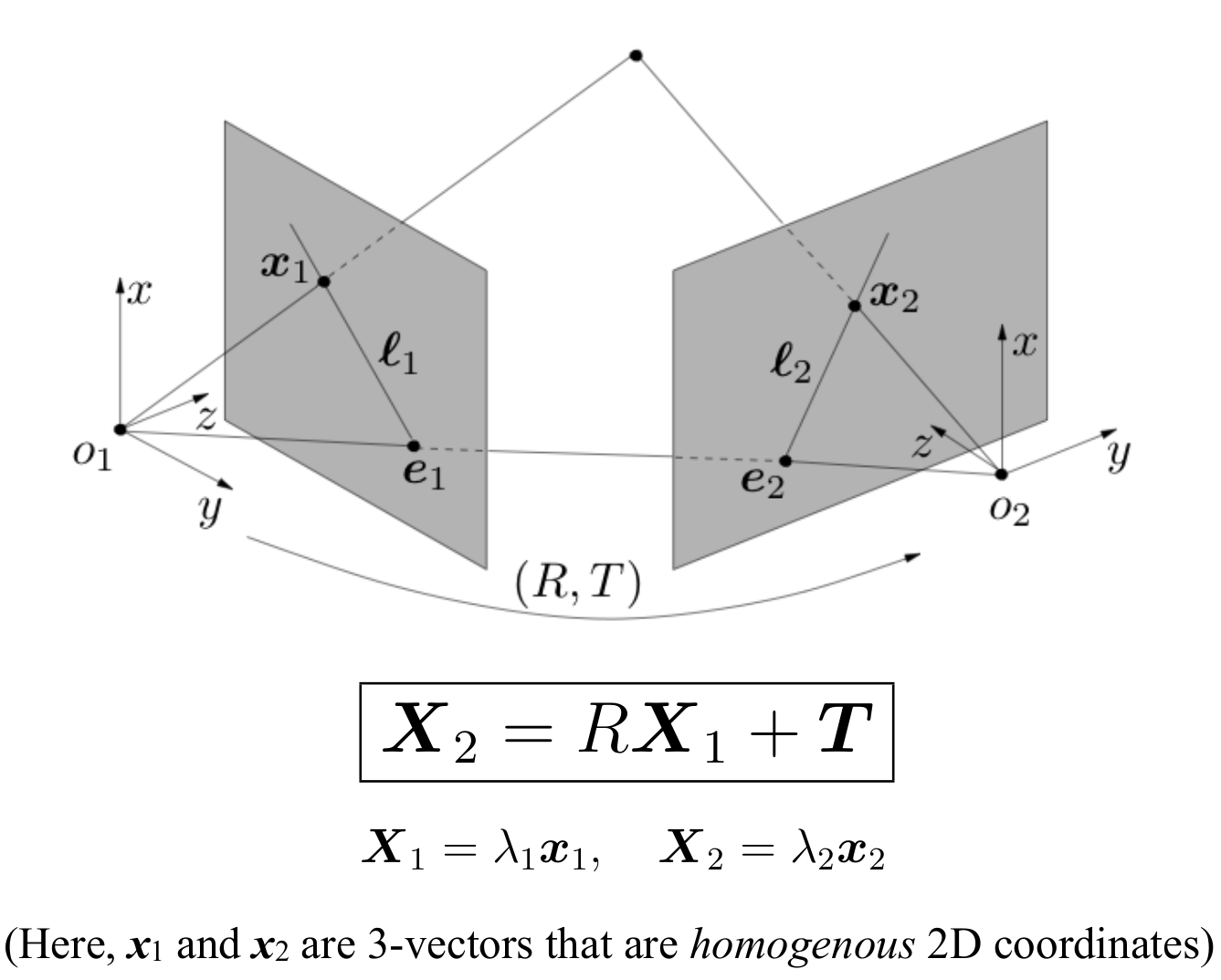
Longuet Higgins Derivation
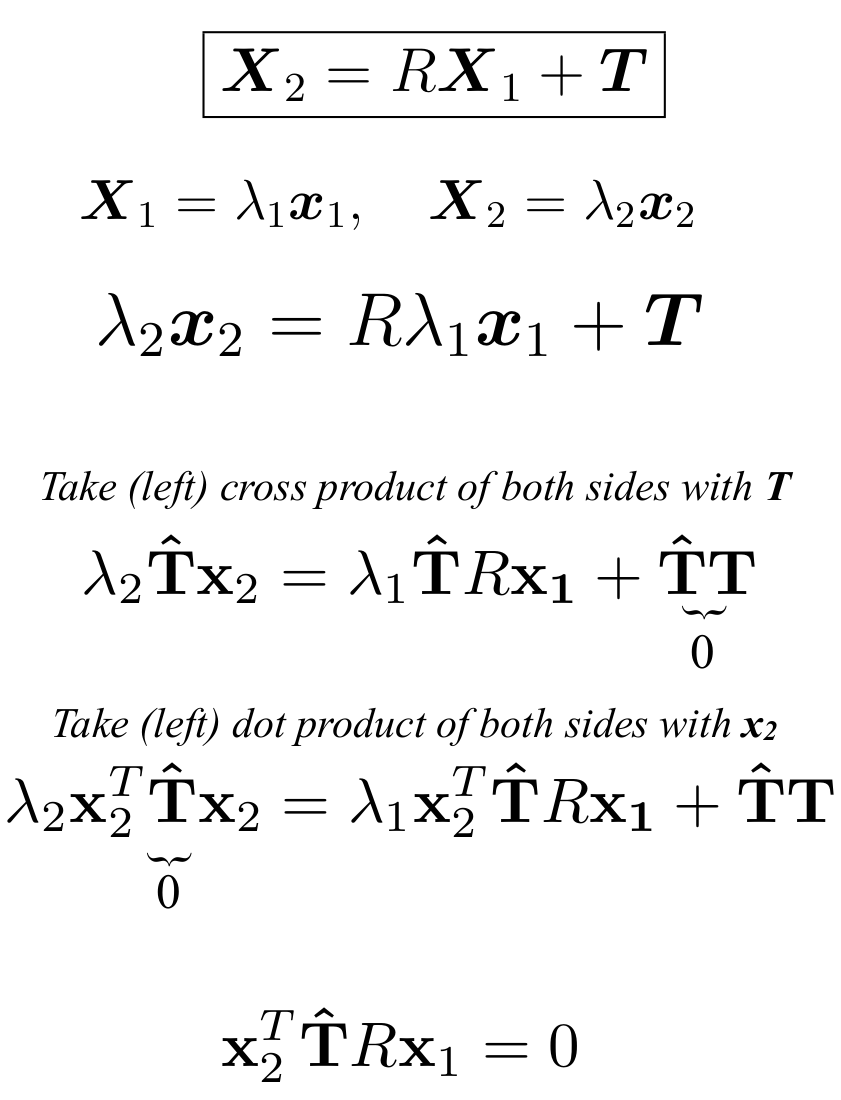
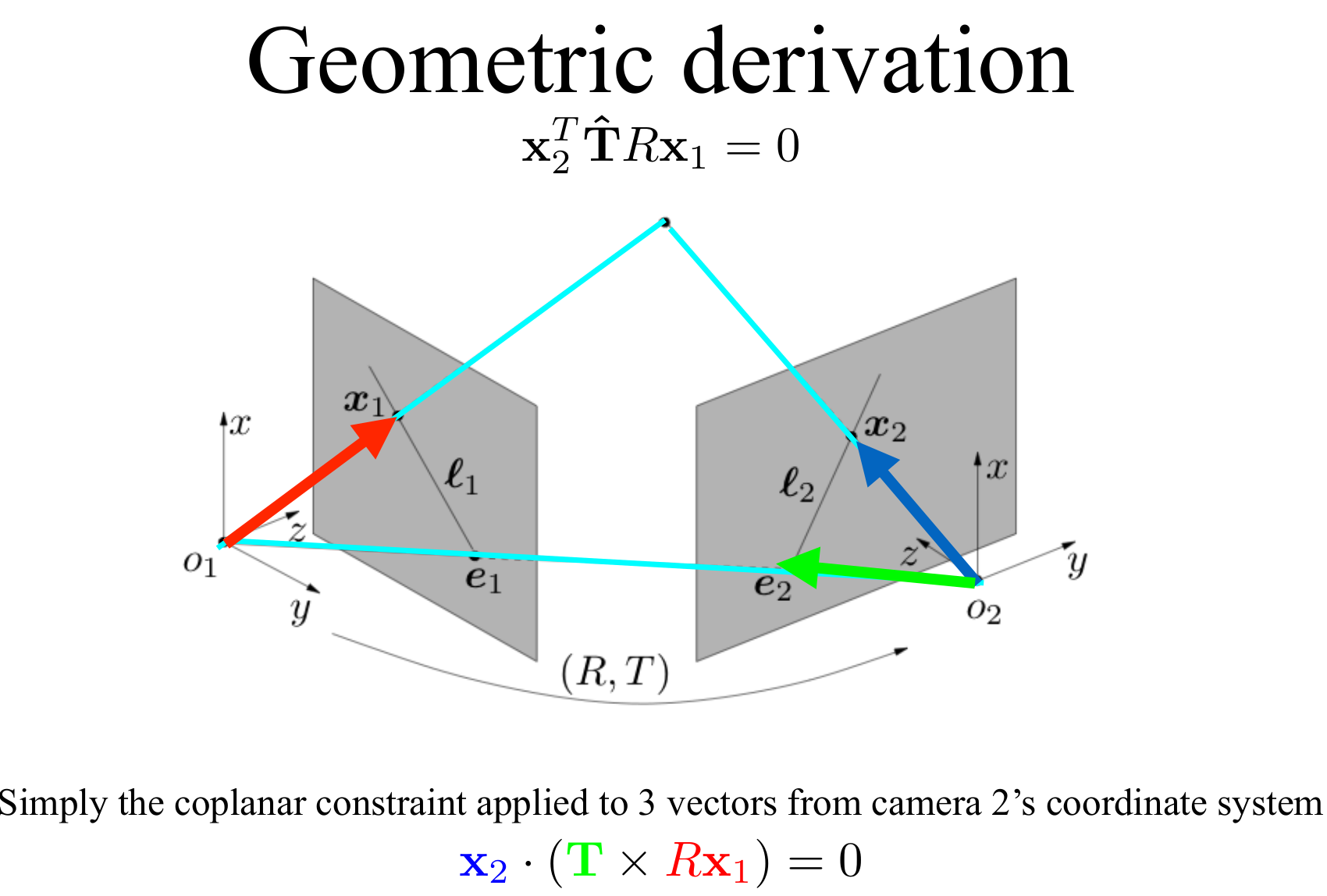
The above derivation tells us in simplicity:
- The volume of the parallelpiped (as seen previously is defined by a.(b x c)) is zero
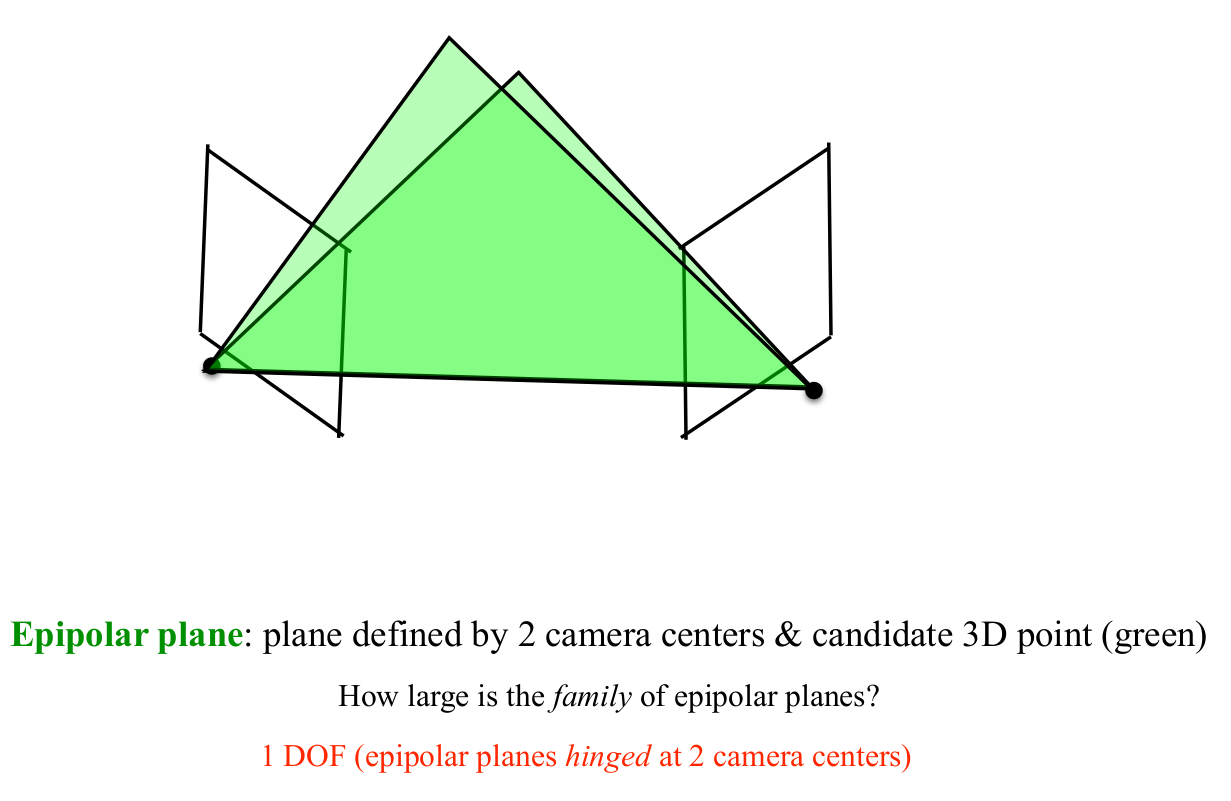
- This means that three vectors are in one plane
- Which makes sense since the epipolar plane is what connects the 2 camera centers and the 3D point
Difference Between Essential Matrix and Homography Matrix
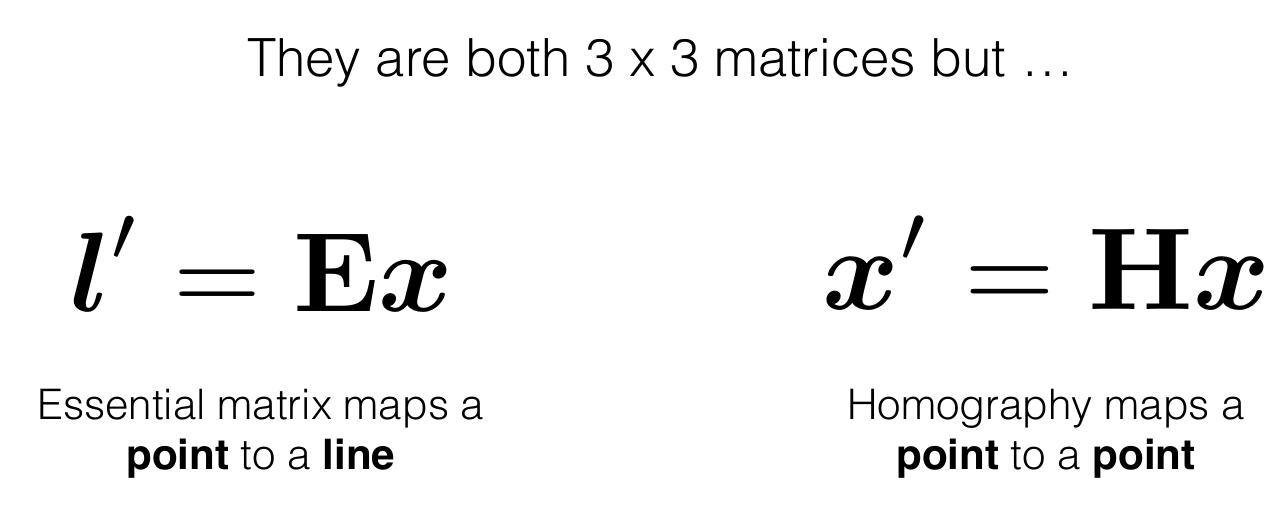
How does this Essential Matrix map a point to a line (where is the math?)

Fundamental Matrix

Structure From Motion Step 1: Estimating Fundamental Matrix:
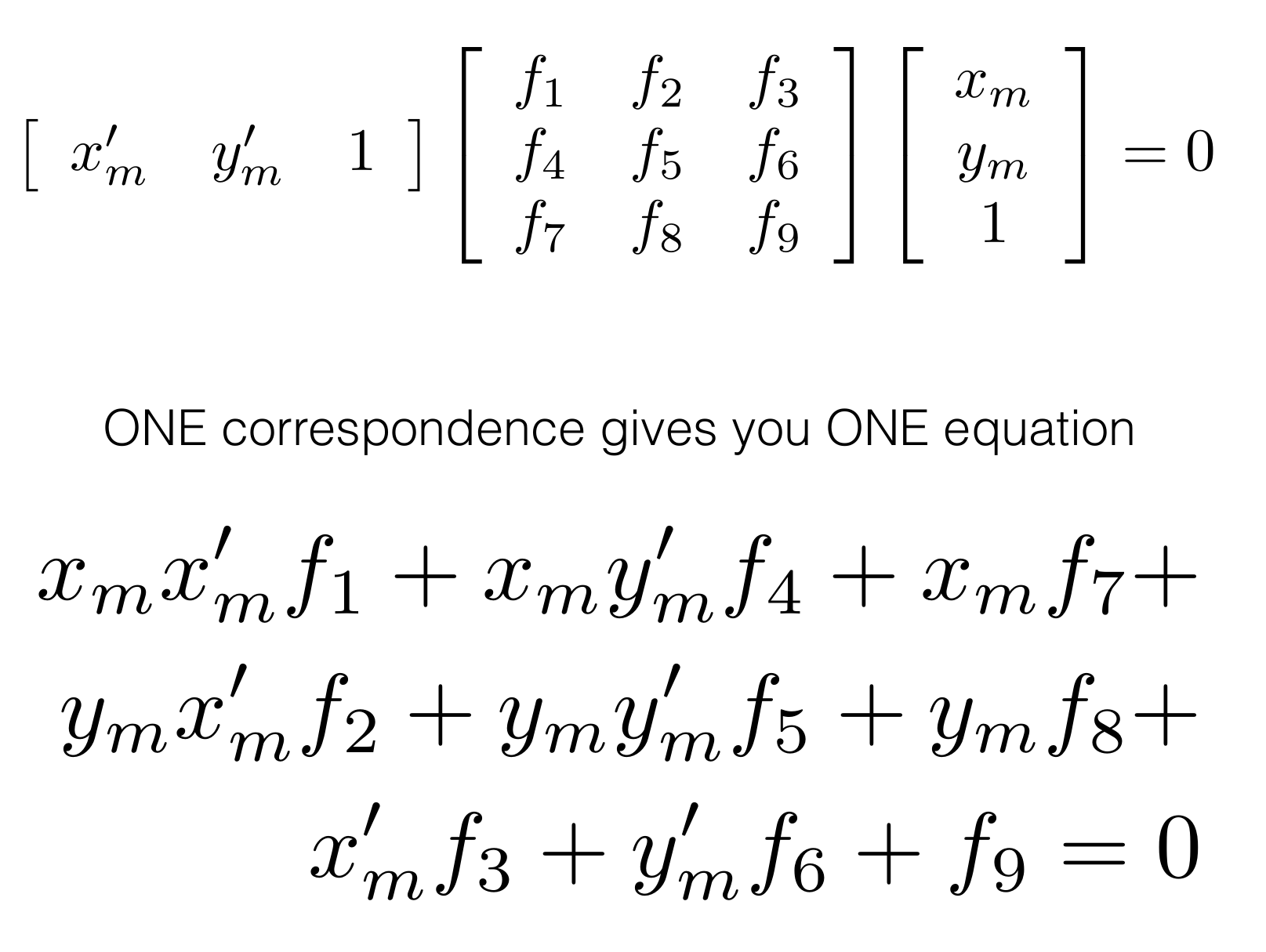

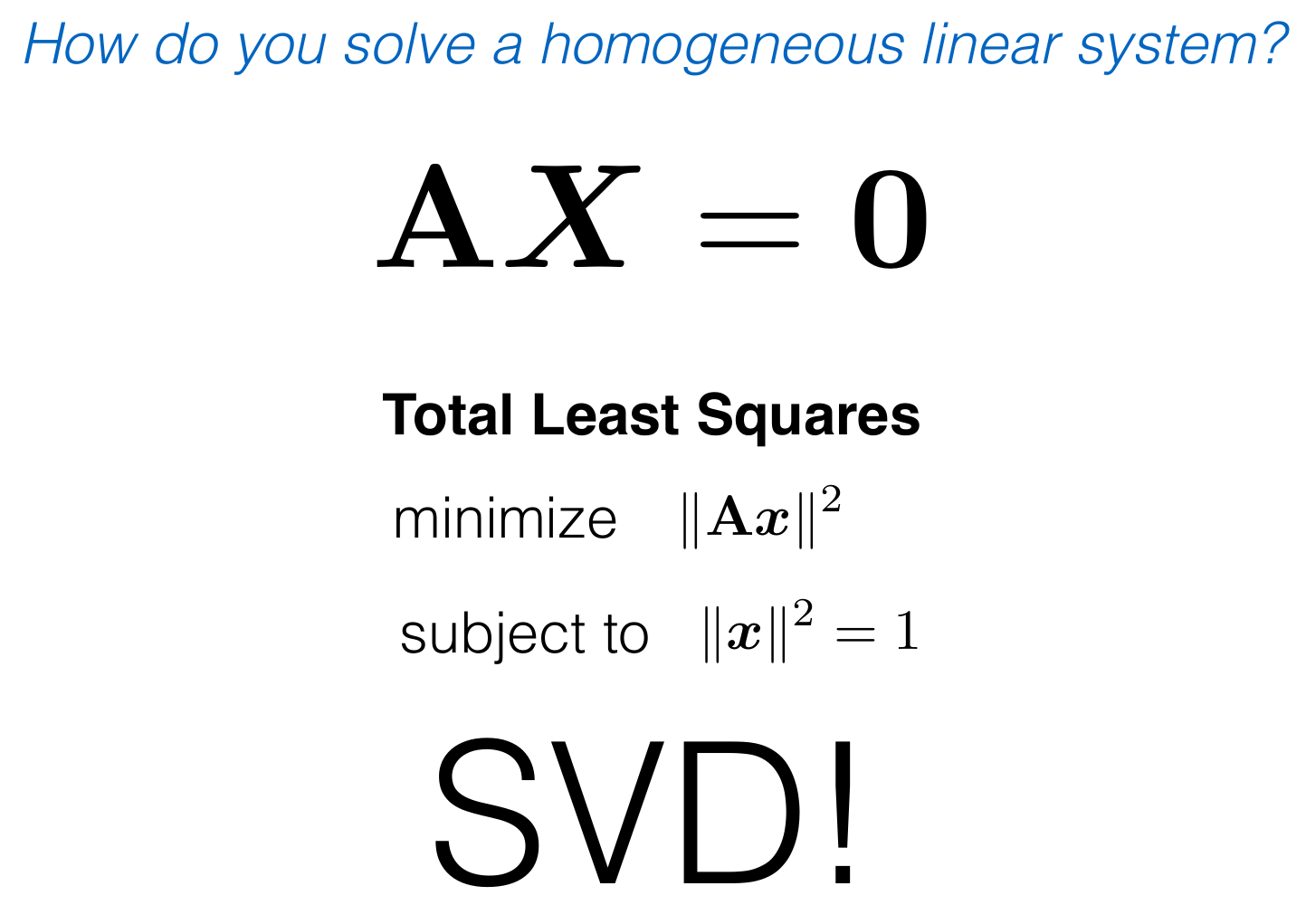

We are given two images of the same object from two different views:


'''
Q2.1: Eight Point Algorithm
Input: pts1, Nx2 Matrix
pts2, Nx2 Matrix
M, a scalar parameter computed as max (imwidth, imheight)
Output: F, the fundamental matrix
HINTS:
(1) Normalize the input pts1 and pts2 using the matrix T.
(2) Setup the eight point algorithm's equation.
(3) Solve for the least square solution using SVD.
(4) Use the function `_singularize` (provided) to enforce the singularity condition.
(5) Use the function `refineF` (provided) to refine the computed fundamental matrix.
(Remember to usethe normalized points instead of the original points)
(6) Unscale the fundamental matrix
'''
def eightpoint(pts1, pts2, M):
"""
Compute the normalized coordinates
and also the fundamental matrix using computeH
Args:
x1 (Mx2): the matched locations of corners in img1
x2 (Mx2): the matched locations of corners in img2
Returns:
F2to1: Fundamental matrix after denormalization
"""
# Compute the centroid of the points
x1, x2 = pts1, pts2
# Doing the M normaliazation
moved_scaled_x1 = x1/M
moved_scaled_x2 = x2/M
t = np.diag([1/M, 1/M, 1])
# Compute Fundamental Matrix
F = computeF(moved_scaled_x1, moved_scaled_x2)
# Refine and then enforce singularity constraint
F = _singularize(F)
F = refineF(F, moved_scaled_x1, moved_scaled_x2)
# Denormalization
F2to1 = np.matmul(t.T, (F @ t))
F2to1 = F2to1/F2to1[2,2]
return F2to1
def computeF(x1, x2):
"""
Computes the fundamental based on
matching points in both images
Args:
x1: keypoints in image 1
x2: keypoints in image 2
Returns:
H2to1: the fundamental matrix
"""
# Define a dummy H matrix
A_build = []
# Define the A matrix for (Ah = 0) (A matrix size = N*2 x 9)
for i in range(x1.shape[0]):
row_1 = np.array([ x2[i,0]*x1[i,0], x2[i,0]*x1[i,1], x2[i,0], x2[i,1]*x1[i,0], x2[i,1]*x1[i,1], x2[i,1], x1[i,0], x1[i,1], 1])
A_build.append(row_1)
A = np.stack(A_build, axis=0)
# Do the least squares minimization to get the homography matrix
# this is done as eigenvector coresponding to smallest eigen value of A`A = H matrix
u, s, v = np.linalg.svd(A)
# here the linalg.svd gives v_transpose
# but we need just V therefore we again transpose
F2to1 = np.reshape(v.T[:,-1], (3,3))
return F2to1
def check_and_create_directory(dir_path, create):
"""
Checks for existing directories and creates if unavailable
[input]
* dir_path : path to be checked
* create : tag to specify only checking path or also creating path
"""
if create == 1:
if not os.path.exists(dir_path):
os.makedirs(dir_path)
else:
if not os.path.exists(dir_path):
warnings.warn(f'following path could not be found: {dir_path}')
if __name__ == "__main__":
correspondence = np.load('data/some_corresp.npz') # Loading correspondences
intrinsics = np.load('data/intrinsics.npz') # Loading the intrinscis of the camera
K1, K2 = intrinsics['K1'], intrinsics['K2']
pts1, pts2 = correspondence['pts1'], correspondence['pts2']
im1 = plt.imread('data/im1.png')
im2 = plt.imread('data/im2.png')
F = eightpoint(pts1, pts2, M=np.max([*im1.shape, *im2.shape]))
print("the fundamental matrix found was \n", F)
# Q2.1
out_dir = "/home/sush/CMU/Assignment_Sem_1/CV_A/Assignment_4/code/outputs"
check_and_create_directory(out_dir, create=1)
np.savez_compressed(
os.path.join(out_dir, 'q2_1.npz'),
F,
np.max([*im1.shape, *im2.shape])
)
displayEpipolarF(im1, im2, F)
Output: 
Estimate Essential Matrix from Fundamental Matrix (given K1 and K2)
'''
Q3.1: Compute the essential matrix E.
Input: F, fundamental matrix
K1, internal camera calibration matrix of camera 1
K2, internal camera calibration matrix of camera 2
Output: E, the essential matrix
'''
def essentialMatrix(F, K1, K2):
E = (K2.T @ F) @ K1
E = E/E[2,2]
print("rank of E is", np.linalg.matrix_rank(E))
return E
if __name__ == "__main__":
correspondence = np.load('data/some_corresp.npz') # Loading correspondences
intrinsics = np.load('data/intrinsics.npz') # Loading the intrinscis of the camera
K1, K2 = intrinsics['K1'], intrinsics['K2']
pts1, pts2 = correspondence['pts1'], correspondence['pts2']
im1 = plt.imread('data/im1.png')
im2 = plt.imread('data/im2.png')
# ----- TODO -----
# YOUR CODE HERE
F = eightpoint(pts1, pts2, M=np.max([*im1.shape, *im2.shape]))
E = essentialMatrix(F, K1, K2)
print("E is \n", E)
Triangulation
triangulate3D
- Here we fix one camera (extrinsic matrix = Identity matrix). Now, we know correspondence points in image1 and image2.
- Using that we found the Fundamental Matrix
Now, to estimate the 3D location of these points, we need
- Camera matrices (extrinsic*intrinsic) for both cameras M1 and M2
- Image points (x,y) which correspond to each other
- Direct Linear Transform
DLT was mentioned above, but small recap: 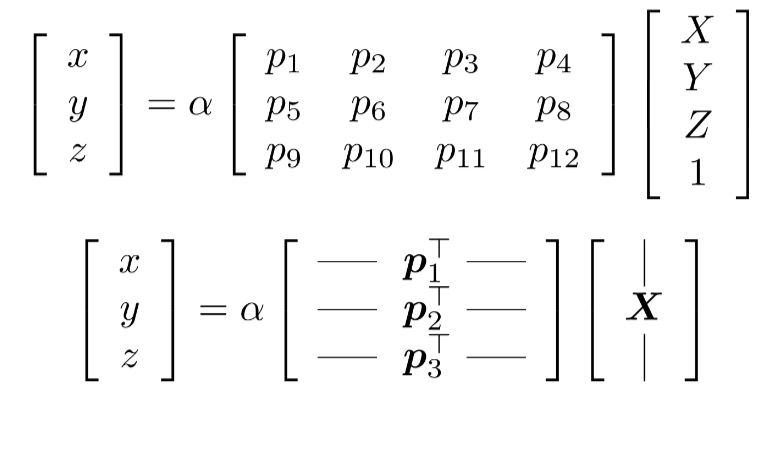

After finding the 3D points, we will reproject them back onto the image and compare them with our original correspondence points (which we either manually selected or got from some keypoint detector like ORB or BRIEF)
The formula for reprojection error in this case is:
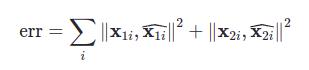
def triangulate(C1, pts1, C2, pts2):
"""
Find the 3D coords of the keypoints
We are given camera matrices and 2D correspondences.
We can therefore find the 3D points (refer L17 (Camera Models) of CV slides)
Note. We can't just use x = PX to compute the 3D point X because of scale ambiguity
i.e the ambiguity can be rep. as x = alpha*Px (we cannot find alpha)
Therefore we need to do DLT just like the case of homography
(see L14 (2D transforms) CVB slide 61)
Args:
C1 : the 3x4 camera matrix of camera 1
pts1 : img coords of keypoints in camera 1 (Nx2)
C2 : the 3x4 camera matrix of camera 2
pts2 : img coords of keypoints in camera 2 (Nx2)
Returns:
P : the estimated 3D point for the given pair of keypoint correspondences
err : the reprojection error
"""
P = np.zeros(shape=(1,3))
err = 0
for i in range(len(pts1)):
# get the camera 1 matrix
p1_1 = C1[0,:]
p2_1 = C1[1,:]
p3_1 = C1[2,:]
# get the camera 2 matrix
p1_2 = C2[0,:]
p2_2 = C2[1,:]
p3_2 = C2[2,:]
x, y = pts1[i,0], pts1[i,1]
x2, y2 = pts2[i,0], pts2[i,1]
# calculate the A matrix for this point correspondence
A = np.array([y*p3_1 - p2_1 , p1_1 - x*p3_1 , y2*p3_2 - p2_2 , p1_2 - x2*p3_2])
u, s, v = np.linalg.svd(A)
# here the linalg.svd gives v_transpose
# but we need just V therefore we again transpose
X = v.T[:,-1]
# print("X is", X)
X = X.T
X = np.expand_dims(X,axis=0)
# print("X after transpose and expand is", X)
# convert X to homogenous coords
X = X/X[0,3]
# print("X after normalizing is", X)
P = np.concatenate((P, X[:,0:3]), axis=0)
X = X.T
# find the error for this projection
# 3x1 = 3x4 . 3x1
pt_1 = ((C1 @ X)/(C1 @ X)[2,0])[0:2,0]
pt_2 = ((C2 @ X)/(C2 @ X)[2,0])[0:2,0]
# calculate the reporjection error
err += np.linalg.norm(pt_1 - pts1[i,:])**2 + np.linalg.norm(pt_2 - pts2[i,:])**2
print("error in this iteration is", err)
P = P[1:,:]
return P, err
Summary
- Given two camera matrices and keypoint correspondences for two views, we triangulated the point (found 3D point)
- We found the reprojection error for this estimated 3D point
Using Triangulate to Find Second Camera Matrix after fixing First Camera Matrix = Identity
Previsously we saw that we need an M2 to triangulate, but we don’t have an M2 yet :/.
However, since our first camera is fixed (identity) we can find the camera matrix M2 of our second camera as:
def camera2(E):
U,S,V = np.linalg.svd(E)
m = S[:2].mean()
E = U.dot(np.array([[m,0,0], [0,m,0], [0,0,0]])).dot(V)
U,S,V = np.linalg.svd(E)
W = np.array([[0,-1,0], [1,0,0], [0,0,1]])
if np.linalg.det(U.dot(W).dot(V))<0:
W = -W
M2s = np.zeros([3,4,4])
M2s[:,:,0] = np.concatenate([U.dot(W).dot(V), U[:,2].reshape([-1, 1])/abs(U[:,2]).max()], axis=1)
M2s[:,:,1] = np.concatenate([U.dot(W).dot(V), -U[:,2].reshape([-1, 1])/abs(U[:,2]).max()], axis=1)
M2s[:,:,2] = np.concatenate([U.dot(W.T).dot(V), U[:,2].reshape([-1, 1])/abs(U[:,2]).max()], axis=1)
M2s[:,:,3] = np.concatenate([U.dot(W.T).dot(V), -U[:,2].reshape([-1, 1])/abs(U[:,2]).max()], axis=1)
return M2s
Note: The above function gives Four possible values for M2
Why the 4 options?
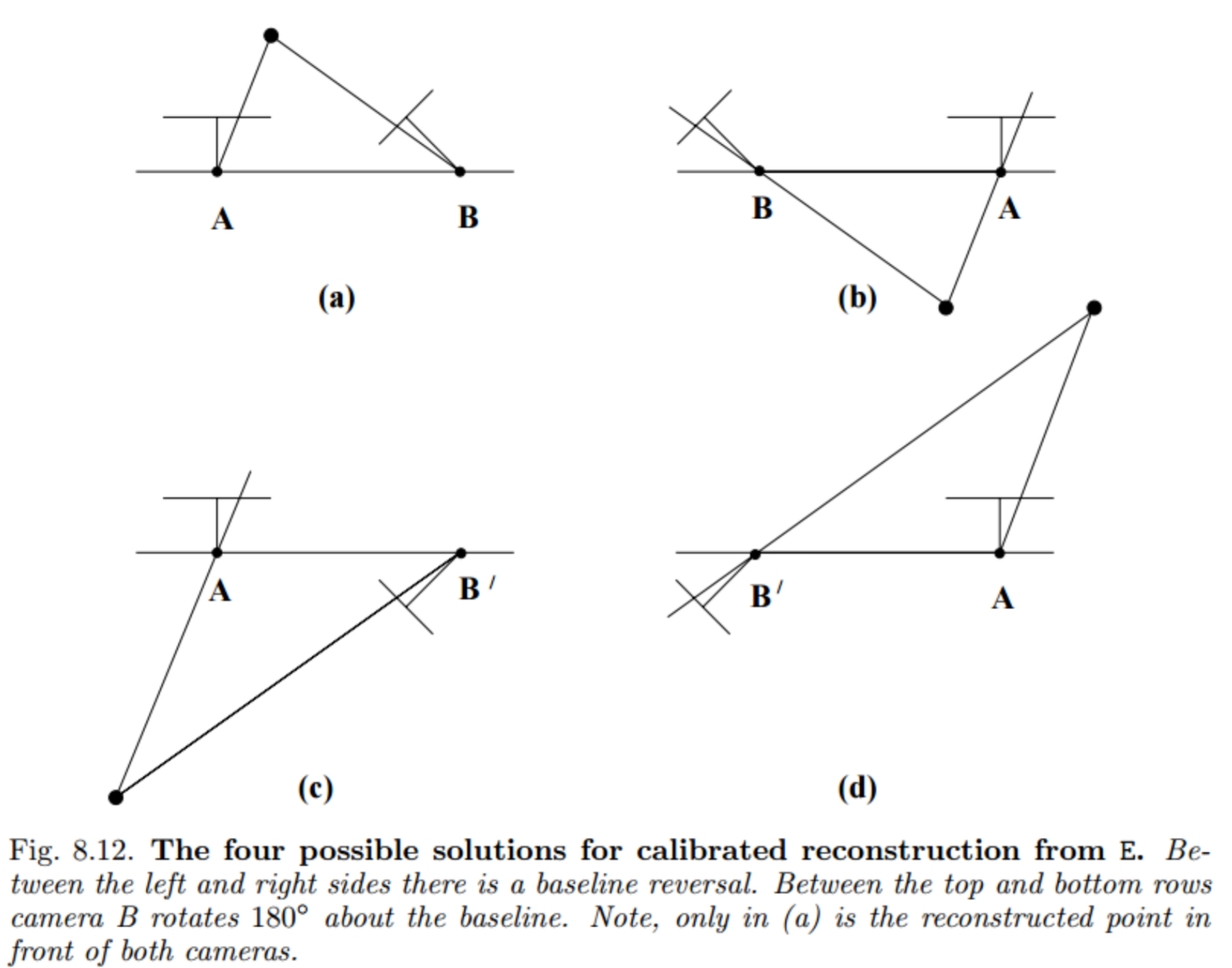
Now there are 2 checks we can use to find which is the right camera:
- Determinant(Rotation component of M2) = 1 (so that the rotation belongs to SO(3))
- All Z values should be positive (i.e. the 3D point should be in front of both the cameras right?)
Combining the above two functions
Now we have point correspondences, M1 and 4 M2’s. Therefore we’ll try to triangulate points based on the correct criteria for camera orientations. Additionally we’ll also try to minimize reprojection error:
# iterate over M1(fixed) and M2(4 possibilites) by passing them to triangulate
for i in range(M2.shape[2]):
M2_current = M2[:,:,i]
# build the C1 and C2:
pts_in_3d, err = triangulate((K1 @ M1), pts1, (K2 @ M2_current), pts2)
if err < err_min and (np.where(pts_in_3d[:,2] < 0)[0].shape[0] == 0):
print("satisfies the error criteria")
err_min = err
best_M2_i = i
best_pts_3d = pts_in_3d
if (best_M2_i is not None) and (best_pts_3d is not None):
print("min err is", err_min)
# return M2, C2, w(3d points), M1, C1
return M2[:,:,best_M2_i], (K2 @ M2[:,:,best_M2_i]), best_pts_3d, M1, (K1 @ M1) # last entry is C1
Finally we all together have:
- our best_3d_points
- correct M2 matrix
Results of Triangulation on Input Images
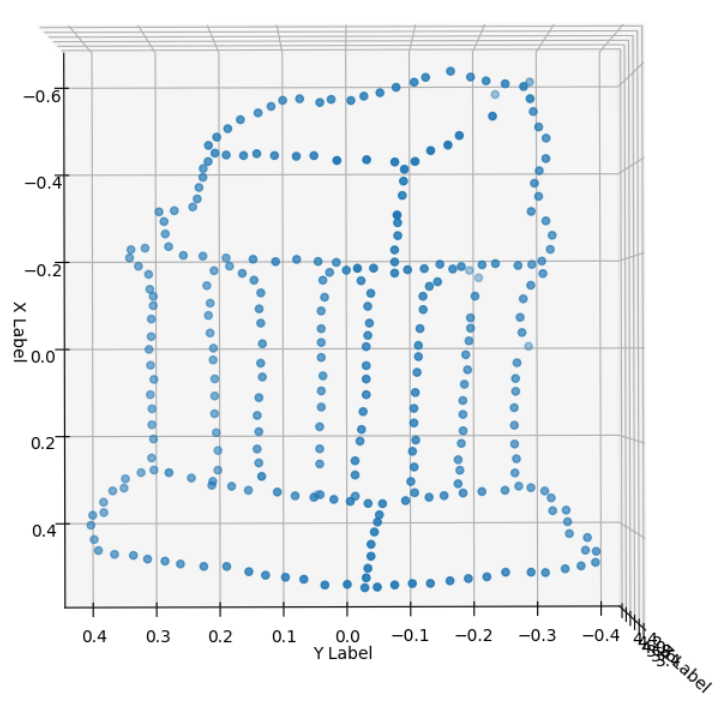
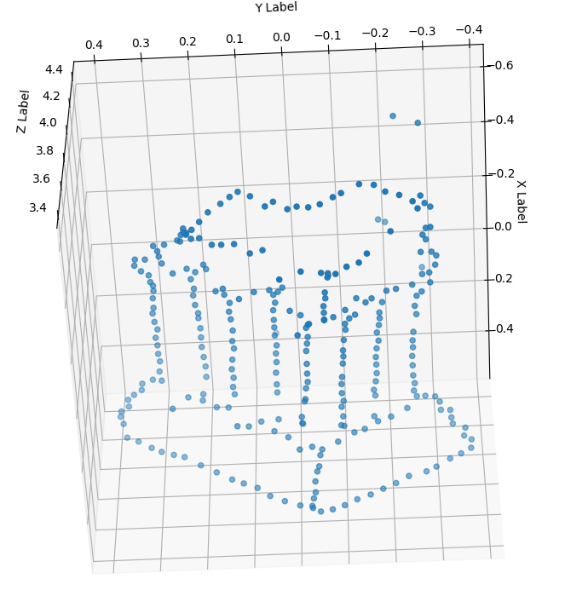
Bundle Adjustment
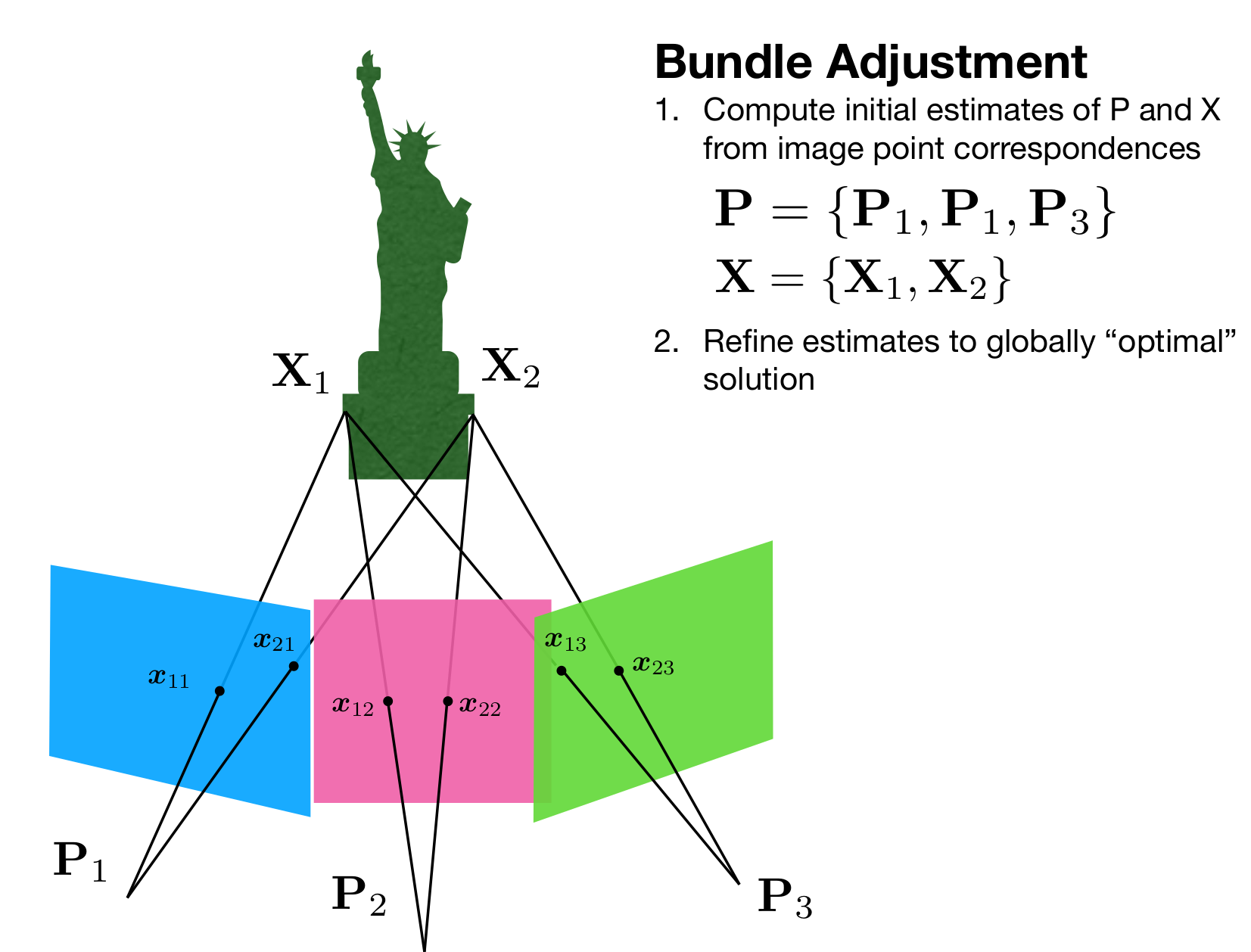
We know that the error in the triangulation is basically difference between the projection of a 3D point and the actual point in 2D on the image. Now, we will move around the 3D points slightly and check in which orientation the reprojection error comes to a global minimum. The formula for the above operation is shown below:

The process we will follow now is very code specific. An explanation for only this below code is shown, where we will only be minimizing the rotation and translation (M2 matrix) error.
High level procedure
- Use the 2D point correspondences to find the Fundamental Matrix (along with RANSAC to find the inlier points)
- Use the inliers to find our best F (fundamental matrix)
- Compute an initial guess for M2 by using our old findM2 function
- Now, the above function would have given us 3D points (P_init) and an M2_init
- Now, we have compiled the following:
- M1 and K1
- M2_init and K2
- F and E (E = (K2.T @ F) @ K1)
Having the above content, we will need to derive our reprojection error. We will do this in the RodriguesResidual function:
RodriguesResidual: rodriguesResidual(x, K1, M1, p1, K2, p2)
- x basically contains the translation and rotation of camera2. We can therefore get M2 from x
- We can find the camera matrices C1 = K1 @ M1, C2 = K2 @ M2

- Use the above equation to get p1’ and p2’
- Compare p1’ and p1, p2’ and p2, to get the reprojection error we need in both cameras

Now we have a function which will give us reprojection error for a given M2 matrix. Now lets see how we’ll use this reporjection error to optimize our M2
Optimization of M2
Now that we have a function which will give us reprojection error for any given M2, lets minimize this error by moving around our 3D points slightly such that our reprojection error (for all points cumulative) reduces
We do this using the scipy.optimize.minimize function
# just some repackaging/preprocessing to give x to rodriguesResidual
x0 = P_init.flatten()
x0 = np.append(x0, r2_0.flatten())
x0 = np.append(x0, t2_0.flatten())
# optimization step
x_opt, _ = scipy.optimize.minimze(rodriguesResidual, x0, args=(K1, M1, p1, K2, p2))
Finally our x_opt i.e x_optimal will have the correct rotation and translation of camera 2 and the corrected 3D points
'''
Q5.3 Bundle adjustment.
Input: K1, the intrinsics of camera 1
M1, the extrinsics of camera 1
p1, the 2D coordinates of points in image 1
K2, the intrinsics of camera 2
M2_init, the initial extrinsics of camera 1 (get this from findM2)
p2, the 2D coordinates of points in image 2
P_init, the initial 3D coordinates of points (get this also from findM2)
Output: M2, the optimized extrinsics of camera 1
P2, the optimized 3D coordinates of points
o1, the starting objective function value with the initial input
o2, the ending objective function value after bundle adjustment
Hints:
(1) Use the scipy.optimize.minimize function to minimize the objective function, rodriguesResidual.
You can try different (method='..') in scipy.optimize.minimize for best results.
'''
def bundleAdjustment(K1, M1, p1, K2, M2_init, p2, P_init):
# given M2_init decompose it into R and t
R2 = M2_init[:,0:3]
t2 = M2_init[:,3]
r2 = invRodrigues(R2)
x_start = P_init.flatten()
x_start = np.append(x_start, np.append(r2.flatten(), t2))
obj_start = rodriguesResidual(x_start, K1, M1, p1, K2, p2)
print("x_start shape is", x_start.shape)
# optimization step
from scipy.optimize import minimize
x_optimized_obj = minimize(residual_norm, x_start, args=(K1, M1, p1, K2, p2), method='Powell')
print("x_end shape is", x_optimized_obj.x.shape)
x_optimized = x_optimized_obj.x
obj_end = rodriguesResidual(x_optimized, K1, M1, p1, K2, p2)
# recompute the M2 and P
# decompose x
P_final = x_optimized[0:-6]
P_shape_req = int(P_final.shape[0]/3)
P_final = np.reshape(P_final, newshape=(P_shape_req,3))
r2_final = x_optimized[-6:-3]
# reshape to 3x1 to feed to inverse rodrigues
r2_final = r2_final.reshape(3,1)
# reshape translation matrix to combine in transformation matrix
t2_final = x_optimized[-3:].reshape(3,1)
# compose the C2 matrix
R2_final = rodrigues(r2_final)
M2_final = np.hstack((R2_final, t2_final))
return M2_final, P_final, obj_start, obj_end
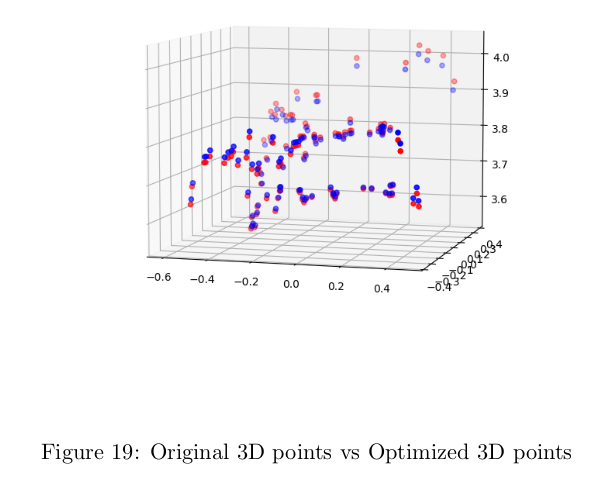
Results on optimizing points after bundle adjustment
Final Pipeline Including RANSAC
if __name__ == "__main__":
np.random.seed(1) #Added for testing, can be commented out
some_corresp_noisy = np.load('data/some_corresp_noisy.npz') # Loading correspondences
intrinsics = np.load('data/intrinsics.npz') # Loading the intrinscis of the camera
K1, K2 = intrinsics['K1'], intrinsics['K2']
noisy_pts1, noisy_pts2 = some_corresp_noisy['pts1'], some_corresp_noisy['pts2']
im1 = plt.imread('data/im1.png')
im2 = plt.imread('data/im2.png')
templeCoords = np.load('data/templeCoords.npz')
temple_pts1 = np.hstack([templeCoords["x1"], templeCoords["y1"]])
#? getting the F matrix from noisy correspondences
M = np.max([*im1.shape, *im2.shape])
F, inliers = ransacF(noisy_pts1, noisy_pts2, M, im1, im2)
inlier_pts1, inlier_pts2 = inliers[0], inliers[1]
print("shape of noisy_pts1 is", noisy_pts1.shape)
print("shape of inlier_pts1 is", inlier_pts1.shape)
F_naieve = eightpoint(noisy_pts1, noisy_pts2, M)
# use displayEpipolarF to compare how ransac_F and naieve_F behave
# displayEpipolarF(im1, im2, F)
# displayEpipolarF(im1, im2, F_naieve)
# Simple Tests to verify your implementation:
from scipy.spatial.transform import Rotation as sRot
rotVec = sRot.random()
mat = rodrigues(rotVec.as_rotvec())
assert(np.linalg.norm(rotVec.as_rotvec() - invRodrigues(mat)) < 1e-3)
assert(np.linalg.norm(rotVec.as_matrix() - mat) < 1e-3)
#? Getting the initial guess for M2 and P
# Assuming the rotation and translation of camera1 is zero
M1 = np.array([[1,0,0,0],[0,1,0,0],[0,0,1,0]])
M2_init, C2, P_init, M1, C1 = findM2(F, inlier_pts1, inlier_pts2, intrinsics)
print("M2 shape is", M2_init)
# Optimize the M2
M2_final, P_final, start_obj, end_obj = bundleAdjustment(
K1,
M1,
inlier_pts1,
K2,
M2_init,
inlier_pts2,
P_init
)
print("error before optimization is", np.linalg.norm(start_obj)**2)
print("error after optimization is", np.linalg.norm(end_obj)**2)
# compare the old M2 to optimized M2
plot_3D_dual(P_init, P_final)
Effects of RANSAC
RANSAC was used even before bundle adjustment, to remove noisy coorespondences for the initial best gues of the Fundamental Matrix.
def ransacF(pts1, pts2, M, im1, im2, nIters=100, tol=10):
"""
Every iteration we init a Fundamental matrix using 4 corresponding
points and calculate number of inliers. Finally use the Homography
matrix which had max number of inliers (and these inliers as well)
to find the final Fundamental matrix
Args:
pts1: location of matched points in image1
pts2: location of matched points in image2
opts: user inputs used for distance tolerance in ransac
Returns:
bestH2to1 : The Fundamental matrix with max number of inliers
inlier_points : Final list of inliers found for best RANSAC iteration
"""
max_iters = nIters # the number of iterations to run RANSAC for
inlier_tol = tol # the tolerance value for considering a point to be an inlier
locs1 = pts1
locs2 = pts2
# define size of both locs1 and locs2
num_rows = locs1.shape[0]
# define a container for keeping track of inlier counts
final_inlier_count = 0
final_distance_error = 10000000000
#? Create a boolean vector of length N where 1 = inlier and 0 = outlier
print("Computing RANSAC")
for i in range(max_iters):
test_locs1 = deepcopy(locs1)
test_locs2 = deepcopy(locs2)
# chose a random sample of 4 points to find H
rand_index = []
rand_index = random.sample(range(int(locs1.shape[0])), k=8)
rand_points_1 = []
rand_points_2 = []
for j in rand_index:
rand_points_1.append(locs1[j,:])
rand_points_2.append(locs2[j,:])
test_locs1 = np.delete(test_locs1, rand_index, axis=0)
test_locs2 = np.delete(test_locs2, rand_index, axis=0)
correspondence_points_1 = np.vstack(rand_points_1)
correspondence_points_2 = np.vstack(rand_points_2)
ref_F = eightpoint(correspondence_points_1, correspondence_points_2, M)
inliers, inlier_count, distance_error, error_state = compute_inliers(ref_F,
test_locs1,
test_locs2,
inlier_tol,
im1,
im2)
if error_state == 1:
continue
if (inlier_count > final_inlier_count):
final_inlier_count = inlier_count
final_inliers = inliers
final_corresp_points_1 = correspondence_points_1
final_corresp_points_2 = correspondence_points_2
final_distance_error = distance_error
final_test_locs1 = test_locs1
final_test_locs2 = test_locs2
if final_distance_error != 100000000:
# print("original point count is", locs1.shape[0])
print("final inlier count is", final_inlier_count)
print("final inlier's cumulative distance error is", final_distance_error)
delete_indexes = np.where(final_inliers==0)
final_locs_1 = np.delete(final_test_locs1, delete_indexes, axis=0)
final_locs_2 = np.delete(final_test_locs2, delete_indexes, axis=0)
final_locs_1 = np.vstack((final_locs_1, final_corresp_points_1))
final_locs_2 = np.vstack((final_locs_2, final_corresp_points_2))
bestH2to1 = eightpoint(final_locs_1, final_locs_2, M)
return bestH2to1, [final_locs_1, final_locs_2]
else:
print("SOMETHING WRONG")
bestH2to1 = eightpoint(correspondence_points_1, correspondence_points_2, M)
return bestH2to1, 0

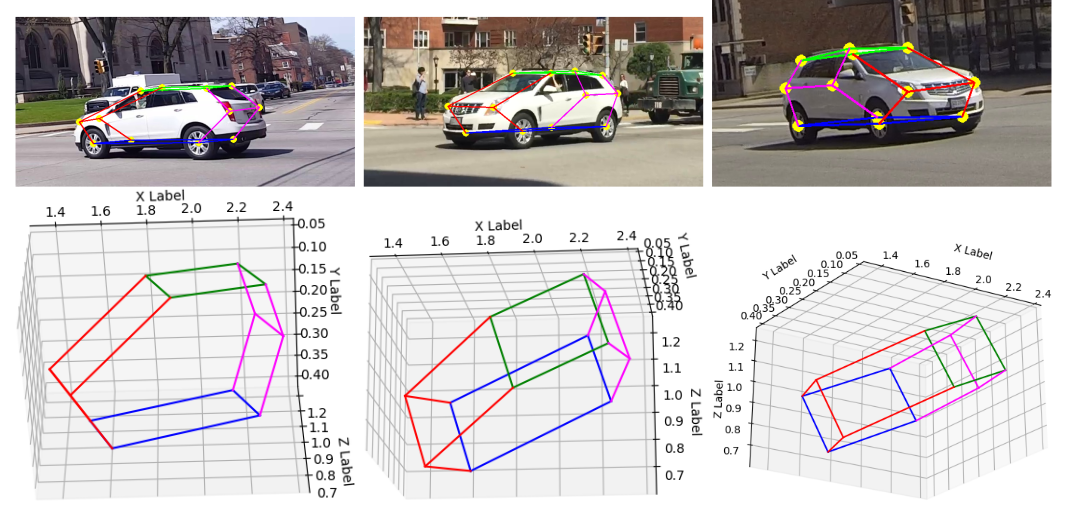
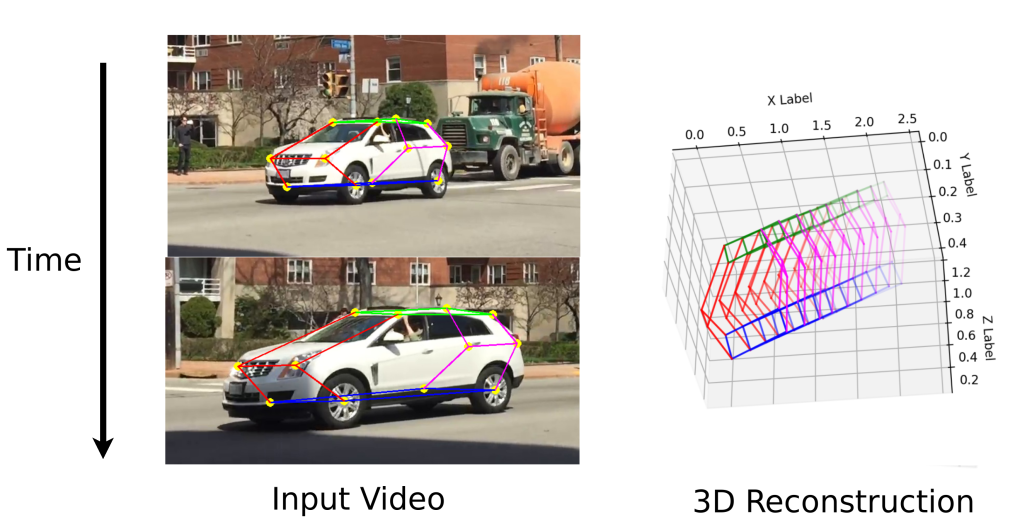
Tracking Real World Objects in 3D

'''
Q6.1 Multi-View Reconstruction of keypoints.
Input: C1, the 3x4 camera matrix
pts1, the Nx3 matrix with the 2D image coordinates and confidence per row
C2, the 3x4 camera matrix
pts2, the Nx3 matrix with the 2D image coordinates and confidence per row
C3, the 3x4 camera matrix
pts3, the Nx3 matrix with the 2D image coordinates and confidence per row
Output: P, the Nx3 matrix with the corresponding 3D points for each keypoint per row
err, the reprojection error.
'''
def MultiviewReconstruction(C1, pts1, C2, pts2, C3, pts3, Thres = 200):
vis_pts_1 = np.where(pts1[:,2] > Thres)
vis_pts_2 = np.where(pts2[:,2] > Thres)
vis_pts_3 = np.where(pts3[:,2] > Thres)
# create a dummy vector to save the 3D points for each corresp 2D pt
pts_3d = np.zeros(pts1.shape)
reproj_error = np.zeros(12)
overlap_all = np.intersect1d(vis_pts_1, vis_pts_2, vis_pts_3)
for i in overlap_all:
pts_cam_1_2, err1 = triangulate(C1, pts1[i,:-1], C2, pts2[i,:-1])
pts_cam_2_3, err2 = triangulate(C2, pts2[i,:-1], C3, pts3[i,:-1])
pts_cam_1_3, err3 = triangulate(C1, pts1[i,:-1], C3, pts3[i,:-1])
avg_pt_i = (pts_cam_1_2 + pts_cam_2_3 + pts_cam_1_3)/3
avg_err = (err1+err2+err3)/3
pts_3d[i,:] = avg_pt_i
reproj_error[i] = avg_err
for i in vis_pts_1[0]:
# print("i is", i)
if i not in overlap_all:
# print("computing", i)
if i in vis_pts_2[0]:
pts_i, err = triangulate(C1, pts1[i,:-1], C2, pts2[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
elif i in vis_pts_3[0]:
pts_i, err = triangulate(C1, pts1[i,:-1], C3, pts3[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
else:
print("point not visible in 2 views")
for i in vis_pts_2[0]:
# print("i is", i)
if i not in overlap_all:
# print("computing", i)
if i in vis_pts_3[0]:
pts_i, err = triangulate(C2, pts2[i,:-1], C3, pts3[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
elif i in vis_pts_1[0]:
pts_i, err = triangulate(C1, pts1[i,:-1], C2, pts2[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
else:
print("point not visible in 2 views")
for i in vis_pts_3[0]:
if i not in overlap_all:
# print("computing", i)
if i in vis_pts_1[0]:
pts_i, err = triangulate(C1, pts1[i,:-1], C3, pts3[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
elif i in vis_pts_2[0]:
pts_i, err = triangulate(C1, pts1[i,:-1], C2, pts2[i,:-1])
pts_3d[i,:] = pts_i
reproj_error[i] = err
else:
print("point not visible in 2 views")
print("pts1 shape is", pts1.shape)
print("3d points shape is", pts_3d.shape)
return pts_3d, reproj_error, [vis_pts_1, vis_pts_2, vis_pts_3]
def MutliviewReconstructionError(x, C1, pts1, C2, pts2, C3, pts3, vis_pts_list):
# decompose x
P_init = x
P_shape_req = int(P_init.shape[0]/3)
P_init = np.reshape(P_init, newshape=(P_shape_req,3))
vis_pts_1 = vis_pts_list[0]
vis_pts_2 = vis_pts_list[1]
vis_pts_3 = vis_pts_list[2]
pts1 = pts1[:,0:2]
pts2 = pts2[:,0:2]
pts3 = pts3[:,0:2]
# list to store error values
err_list = []
# build a sub_P matrix for all visible points in pts1, pts2, pts3
sub_pts1 = np.take(pts1, vis_pts_1, axis=0)[0]
sub_P1 = np.take(P_init, vis_pts_1, axis=0)[0]
sub_pts2 = np.take(pts2, vis_pts_2, axis=0)[0]
sub_P2 = np.take(P_init, vis_pts_2, axis=0)[0]
sub_pts3 = np.take(pts3, vis_pts_3, axis=0)[0]
sub_P3 = np.take(P_init, vis_pts_3, axis=0)[0]
P_list = [sub_P1, sub_P2, sub_P3]
pts_list = [sub_pts1, sub_pts2, sub_pts3]
C_list = [C1, C2, C3]
for i in range(len(P_list)):
P = P_list[i]
p= pts_list[i]
C = C_list[i]
# homogenize P to contain a 1 in the end (P = Nx3 vector)
P_homogenous = np.append(P, np.ones((P.shape[0],1)), axis=1)
# Find the projection of P1 onto image 1 (vectorize)
# Transpose P_homogenous to make it a 4xN vector and left mulitply with C1
# 3xN = 3x4 @ 4XN
p_hat = (C @ P_homogenous.T)
# normalize and transpose to get back to format of p1
p_hat = ((p_hat/p_hat[2,:])[0:2,:]).T
error = np.linalg.norm((p-p_hat).reshape([-1]))**2
err_list.append(error)
err_total = err_list[0] + err_list[1] + err_list[2]
# print("error overall is", err_total)
return err_total
def triangulate(C1, pts1, C2, pts2):
"""
Find the 3D coords of the keypoints
We are given camera matrices and 2D correspondences.
We can therefore find the 3D points (refer L17 (Camera Models) of CV slides)
Note. We can't just use x = PX to compute the 3D point X because of scale ambiguity
i.e the ambiguity can be rep. as x = alpha*Px (we cannot find alpha)
Therefore we need to do DLT just like the case of homography
(see L14 (2D transforms) CVB slide 61)
Args:
C1 : the 3x4 camera matrix of camera 1
pts1 : img coords of keypoints in camera 1 (Nx2)
C2 : the 3x4 camera matrix of camera 2
pts2 : img coords of keypoints in camera 2 (Nx2)
Returns:
P : the estimated 3D point for the given pair of keypoint correspondences
err : the reprojection error
"""
P = np.zeros(shape=(1,3))
err = 0
# get the camera 1 matrix
p1_1 = C1[0,:]
p2_1 = C1[1,:]
p3_1 = C1[2,:]
# get the camera 2 matrix
p1_2 = C2[0,:]
p2_2 = C2[1,:]
p3_2 = C2[2,:]
x, y = pts1[0], pts1[1]
x2, y2 = pts2[0], pts2[1]
# calculate the A matrix for this point correspondence
A = np.array([y*p3_1 - p2_1 , p1_1 - x*p3_1 , y2*p3_2 - p2_2 , p1_2 - x2*p3_2])
u, s, v = np.linalg.svd(A)
# here the linalg.svd gives v_transpose
# but we need just V therefore we again transpose
X = v.T[:,-1]
# print("X is", X)
X = X.T
X = np.expand_dims(X,axis=0)
# print("X after transpose and expand is", X)
# convert X to homogenous coords
X = X/X[0,3]
# print("X after normalizing is", X)
P = np.concatenate((P, X[:,0:3]), axis=0)
X = X.T
# find the error for this projection
# 3x1 = 3x4 . 3x1
pt_1 = ((C1 @ X)/(C1 @ X)[2,0])[0:2,0]
pt_2 = ((C2 @ X)/(C2 @ X)[2,0])[0:2,0]
# calculate the reporjection error
err += np.linalg.norm(pt_1 - pts1)**2 + np.linalg.norm(pt_2 - pts2)**2
# print("error in this iteration is", err)
P = P[1:,:]
return P[0], err
'''
Q6.2 Plot Spatio-temporal (3D) keypoints
:param car_points: np.array points * 3
'''
def plot_3d_keypoint_video(pts_3d_video):
fig = plt.figure()
# num_points = pts_3d.shape[0]
ax = fig.add_subplot(111, projection='3d')
vid_len = len(pts_3d_video)
vals = np.linspace(0.1,1, num=vid_len, endpoint=False)
for i in range(len(pts_3d_video)):
pts_3d = pts_3d_video[i]
for j in range(len(connections_3d)):
index0, index1 = connections_3d[j]
xline = [pts_3d[index0,0], pts_3d[index1,0]]
yline = [pts_3d[index0,1], pts_3d[index1,1]]
zline = [pts_3d[index0,2], pts_3d[index1,2]]
ax.plot(xline, yline, zline, color=colors[j], alpha=vals[i])
np.set_printoptions(threshold=1e6, suppress=True)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
#Extra Credit
if __name__ == "__main__":
pts_3d_video = []
for loop in range(10):
print(f"processing time frame - {loop}")
data_path = os.path.join('data/q6/','time'+str(loop)+'.npz')
image1_path = os.path.join('data/q6/','cam1_time'+str(loop)+'.jpg')
image2_path = os.path.join('data/q6/','cam2_time'+str(loop)+'.jpg')
image3_path = os.path.join('data/q6/','cam3_time'+str(loop)+'.jpg')
im1 = plt.imread(image1_path)
im2 = plt.imread(image2_path)
im3 = plt.imread(image3_path)
data = np.load(data_path)
pts1 = data['pts1']
pts2 = data['pts2']
pts3 = data['pts3']
K1 = data['K1']
K2 = data['K2']
K3 = data['K3']
M1 = data['M1']
M2 = data['M2']
M3 = data['M3']
#Note - Press 'Escape' key to exit img preview and loop further
# img = visualize_keypoints(im2, pts2)
C1 = K1 @ M1
C2 = K2 @ M2
C3 = K3 @ M3
pts_3d, err, vis_pts_list = MultiviewReconstruction(C1, pts1, C2, pts2, C3, pts3)
x_start = pts_3d.flatten()
x_optimized_obj = minimize(MutliviewReconstructionError, x_start, args=(C1, pts1, C2, pts2, C3, pts3, vis_pts_list), method='Powell')
print("x_end shape is", x_optimized_obj.x.shape)
x_optimized = x_optimized_obj.x
P_final = x_optimized
P_shape_req = int(P_final.shape[0]/3)
P_final = np.reshape(P_final, newshape=(P_shape_req,3))
plot_3d_keypoint(P_final)
pts_3d_video.append(P_final)
visualize_keypoints(im1, pts1, Threshold=200)
plot_3d_keypoint_video(pts_3d_video)
out_dir = "/home/sush/CMU/Assignment_Sem_1/CV_A/Assignment_4/code/outputs"
check_and_create_directory(out_dir, create=1)
np.savez_compressed(
os.path.join(out_dir, 'q6_1.npz'),
P_final)