Why Constrained RRT?

As part of my autonomy project, we needed to pickup a tray and place it in a shelf.

Generic RRT helps plan trajectories from say the table -> shelf. However, RRT gives only joint angles which are within the robot’s config space and has no obstacle collisions. In our use-case we needed a plan (trajectory) which ensures that the tray stays level throughout the journey from the table -> shelf.

Formally, the constraints mentioned above are:

Roll = 0
Pitch = 0
Yaw = no constraint

Generic RRT

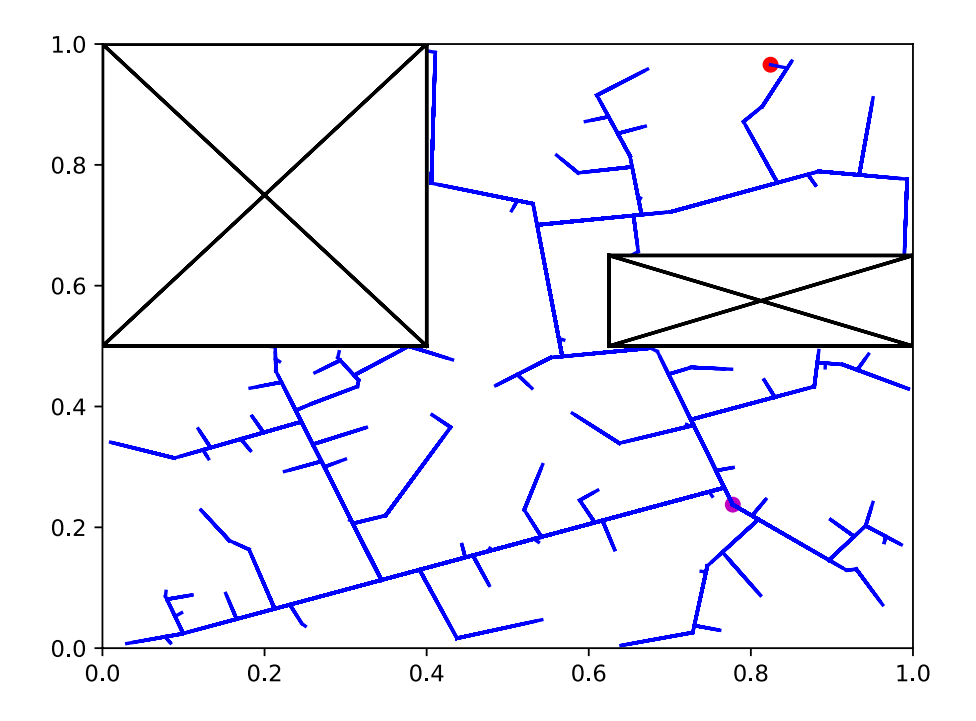
Sampling in Generic RRT

Vanilla RRT uses simple joint constraints, within which it queries for random samples. The image below shows the Franka Panda robot which will be used in this project. The Franka has 8 joints which also includes the end effector.

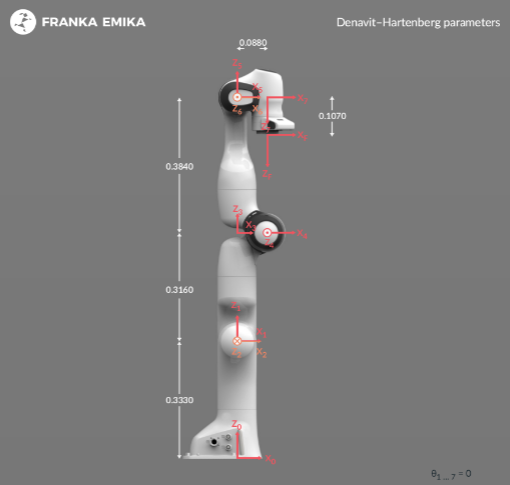
In vanilla RRT, the joints are given some basic constraints (based on design of the robot)

self.qmin=[-2.8973, -1.7628, -2.8973, -3.0718, -2.8973, -0.0175, -2.8973] # NOTE-does not include grippers
self.qmax=[2.8973, 1.7628, 2.8973, -0.0698, 2.8973, 3.7525, 2.8973] # NOTE-does not include gripper

RRT Then works by simply sampling randomly in the limits of qmin and qmax

def SampleRobotConfig(self):
		q=[]
		for i in range(7):
			q.append(self.qmin[i]+(self.qmax[i]-self.qmin[i])*random.random())
		return q

Let’s call new sampled joints as vertices (like nodes in a graph) and any two edges are by edges (like edges in a graph)

Checks on sampled points:

We then check for collisions along these sampled joint angles.
Note. In other methodws like PRM (probabalistic roadmaps), the configuration space is queried beforehand and is stored to reduce search time
However, if we sample vertices that are too far away, we will have to constrain the expansion
We also need to check if one of our vertices is close enough to the goal to say we’ve reached
Note. We also introduce a goal bias by directly setting the sample config = goal config say 2% of the time.

These checks are shown below:

def RRTQuery():

	global FoundSolution
	global plan
	global rrtVertices
	global rrtEdges

	while len(rrtVertices)<3000 and not FoundSolution:

		# TODO : Fill in the algorithm here
		# create a random node (x,y as a 2,1 array)
		qRand = mybot.SampleRobotConfig()

		# introduce the goal bias. (set the random node as goal with a certain prob)
		if np.random.uniform(0,1) < thresh:
			qRand = qGoal

		idNear = FindNearest(rrtVertices, qRand)
		qNear = rrtVertices[idNear]

		qNear, qRand = np.asarray(qNear), np.asarray(qRand)

		# if it's above threshold, move in the direction of the new node, but only upto the
		# threshold (which limits max distance between two nodes)
		while np.linalg.norm(qRand - qNear) > thresh:
			# qConnect = qNear + thres * unit_vector_pointing_towards_qRand
			qConnect = qNear + thresh * ((qRand-qNear) / np.linalg.norm(qRand-qNear))

			if not mybot.DetectCollisionEdge(qConnect, qNear, pointsObs, axesObs):
				rrtVertices.append(qConnect)
				rrtEdges.append(idNear)
				qNear = qConnect

			else:
				break

		# check for collisions
		qConnect = qRand
		if not mybot.DetectCollisionEdge(qConnect, qNear, pointsObs, axesObs):
			# if no collision in new joint angles (qConnect), then add as a valid node and edge
			rrtVertices.append(qConnect)
			rrtEdges.append(idNear)

		# check if the qGoal is close to some node
		idNear = FindNearest(rrtVertices, qGoal)
		# if the qGoal is really close (< 0.025) then we've pretty much reached goal!
		if np.linalg.norm(np.asarray(qGoal) - np.asarray(rrtVertices[idNear])) < 0.025:
			# add the goal node as our final node
			rrtVertices.append(qGoal)
			rrtEdges.append(idNear)
			print("SOLUTION FOUND")
			FoundSolution = True

		print(len(rrtVertices))

Constrained RRT

We saw above some tricks to make simple RRT work. Now, with one small modification we can also make it work in a constrained manner.

Constraining Sampled Points

To constrain the sampled points, we simply project the config space of the sampled points to the constrained config space
This projection was described by Berenson, Siddhartha S. etal
The process of projecting sample_points -> valid_config_space is achieved by gradient descent

In a simple manner, we essentially do the following:

Define a state vector for the end effector
Define a cost function which uses certain elements in the above state vector
Minimize this cost function to obtain the valid config-space needed

In the above picture, the cost function seeks to minimize the roll and pitch of the end effector

The final equation shows the update step (gradient descent)

Defining constraints in code

Projection Function

def project_to_constrain(qRand):
	"""
	Project to make roll and pitch zero where possible. We do this by gradient descent

	Our cost function is C = (3.14 - roll)**2 + pitch**2 (we want to minize roll and pitch)
	NOTE: (3.14 - roll) since we have init roll of 3.14
	"""

	# do forward kinematics and get the roll, pitch at qRand
	roll, pitch, yaw, J = get_roll_pitch_of_rand_pt(qRand)
	# print(f"init roll={roll} and pitch={pitch} and yaw={yaw}")

	if (abs(starting_roll-abs(roll))) > rejection_threshold or \
		(abs(starting_pitch - abs(pitch)) > rejection_threshold):
		return qRand, True

	count = 0

	# while(((starting_roll-abs(roll))**2 + pitch**2 + (starting_yaw - abs(yaw)) > cost_thresh) and count < 1000):
	while(((starting_roll-abs(roll))**2 + (starting_pitch-abs(pitch))**2 > cost_thresh)
       		and count < 1000):
		grad_cost_wrt_xyzrpy = np.expand_dims(np.array([0,0,0, 2*roll, 2*pitch, 0]), axis=1)
		gradient = J.T @ grad_cost_wrt_xyzrpy

		qRand = np.expand_dims(np.array(qRand), axis=1) - learning_rate * gradient
		qRand = np.squeeze(qRand).tolist()
		roll, pitch, yaw, J = get_roll_pitch_of_rand_pt(qRand)
		count += 1

	# print(f"final roll={roll} and pitch={pitch} and yaw={yaw}")

	return qRand, False


def get_roll_pitch_of_rand_pt(qRand):
	# do forward kinematics and get the Tcurr, J at qRand
	Tcurr, J = mybot.ForwardKin_for_check(qRand)
	last_link_rotation = np.asarray(Tcurr[joint_to_constrain])[0:3,0:3]
	r = Rotation.from_matrix(last_link_rotation)
	roll, pitch, yaw = r.as_euler('xyz')

	return roll, pitch, yaw, J

Introducing constraints to RRT

In addition to the steps specified in the algorithm above, I needed to tune some hyperparameters to make it work. Specifically Rejection Threshold, Learning Rate, Cost Threshold.

Even before doing gradient descent, I verify if the end effector state (specifically roll and pitch) are within 1 radian from my goal state (zero roll and zero pitch). This sped up the algorithm, possibly because it takes longer to compute the jacobian and do gradient descent for samples that are too far away from desired state.
Secondly, I needed to tune the learning rate of the gradient descent step
I also had to define a threshold within which the cost function would need to optimize wihtin (it would take forever if I wanted roll^2 + pitch^2 == 0), therefore I let gradient descent to run uptill roll^2 + pitch^2 < 0.2

Implementation

def RRTQuery():

	global FoundSolution
	global plan
	global rrtVertices
	global rrtEdges

	roll, pitch, yaw, J = get_roll_pitch_of_rand_pt(qInit)
	print("starting roll, pitch, and yaw", roll, pitch, yaw)

	# making the assumption that we should find solution within 3000 iterations
	while len(rrtVertices)<10000 and not FoundSolution:

		# TODO : Fill in the algorithm here
		# create a random node (x,y as a 2,1 array)
		qRand = mybot.SampleRobotConfig()

		# introduce the goal bias. (set the random node as goal with a certain prob)
		if np.random.uniform(0,1) < thresh:
			qRand = qGoal

		"""Constrained RRT step"""
		# NOTE: now that we have a qRand, if we want this qRand to be such that the
		# end effector has roll and pitch as zero
		qRand, flag_1 = project_to_constrain(qRand)
		flag_2 = False
		for i in range(len(qRand)):
			if (qRand[i] > mybot.qmax[i] or qRand[i] < mybot.qmin[i]):
				flag_2 = True

		# flag_1 -> being true denotes that we couldn't project
		# flag_2 -> being true denotes that we got infeasible joint angles
		# print(flag_1, flag_2)
		if flag_1 or flag_2:
			continue
		"""End of Constrained RRT"""

		idNear = FindNearest(rrtVertices, qRand)
		qNear = rrtVertices[idNear]

		qNear, qRand = np.asarray(qNear), np.asarray(qRand)

		# if it's above threshold, move in the direction of the new node, but only upto the
		# threshold (which limits max distance between two nodes)
		while np.linalg.norm(qRand - qNear) > thresh:
			# qConnect = qNear + thres * unit_vector_pointing_towards_qRand
			qConnect = qNear + thresh * ((qRand-qNear) / np.linalg.norm(qRand-qNear))

			"""Constrained RRT step"""
			# NOTE: now that we have a qRand, if we want this qRand to be such that the
			# end effector has roll and pitch as zero
			qConnect, flag_1 = project_to_constrain(np.ndarray.tolist(qConnect))
			flag_2 = False
			for i in range(len(qRand)):
				if (qConnect[i] > mybot.qmax[i] or qRand[i] < mybot.qmin[i]):
					flag_2 = True

			# flag_1 -> being true denotes that we couldn't project
			# flag_2 -> being true denotes that we got infeasible joint angles
			# print(flag_1, flag_2)
			if flag_1 or flag_2:
				break
			else:
				qConnect = np.asarray(qConnect)
			"""End of Constrained RRT"""

			if not mybot.DetectCollisionEdge(qConnect, qNear, pointsObs, axesObs):
				rrtVertices.append(qConnect)
				rrtEdges.append(idNear)
				qNear = qConnect

			else:
				break

		# check for collisions
		qConnect = qRand
		if not mybot.DetectCollisionEdge(qConnect, qNear, pointsObs, axesObs):
			# if no collision in new joint angles (qConnect), then add as a valid node and edge
			rrtVertices.append(qConnect)
			rrtEdges.append(idNear)

		# check if the qGoal is close to some node
		idNear = FindNearest(rrtVertices, qGoal)
		# if the qGoal is really close (< 0.025) then we've pretty much reached goal!
		if np.linalg.norm(np.asarray(qGoal) - np.asarray(rrtVertices[idNear])) < 0.025:
			# add the goal node as our final node
			rrtVertices.append(qGoal)
			rrtEdges.append(idNear)
			print("SOLUTION FOUND")
			FoundSolution = True

		print(len(rrtVertices))

Testing in Simulation

The above code was tested using Mujoco simulator. I’ve shown comparisons between vanilla and constrained RRT

Vanilla RRT	Constrained RRT

Testing in Real Life

Acknowledgement

I’d like to thank my team-mate Zack for working beside me throughout this project